Humans seem to have an instinct for music. Certain songs have a quality that makes us want to tap our toes and sing along. We can’t quite say what makes good music, but we know it when we hear it. Sheet music, which tells musicians very precisely which notes to play and when, provides little clue to that mystical ingredient, but Dmitri Tymoczko ’91 has devised a new way to map music that aims to do just that.
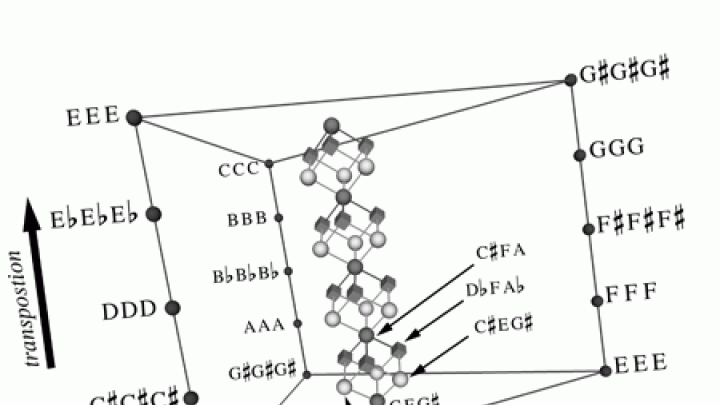
Tymoczko (pronounced tim-OSS-ko), who spent this past academic year as a composer in residence at the Radcliffe Institute for Advanced Study, has developed a way to represent music spatially. Using non-Euclidean geometry and a complex figure, borrowed from string theory, called an orbifold (which can have from two to an infinite number of dimensions, depending on the number of notes being played at once), Tymoczko’s system shows how chords that are generally pleasing to the ear appear in locations close to one another, clustered close to the orbifold’s center. Sounds that the ear identifies as dissonant appear as outliers, closer to the edges.
The system “allows you to translate these half-formed intuitive understandings into very precise, clear language,” says Tymoczko, an assistant professor of music at Princeton. “Personally, I find that incredibly cool.” So, apparently, did Science, which recently published his mathematically based exposition—the only music-theory paper the journal has accepted in its 127-year history.
Tymoczko’s quest didn’t begin with technical complexity. He made his first experimental musical maps using scissors and paper, then graduated to marshmallows connected with toothpicks. When he gives talks today, he hands out school supplies and has each listener assemble a Möbius strip, a rectangular strip of paper given a half twist and then taped together at the ends to form a bracelet-like loop. One trip around the loop lands the tip of a pen back where it began, but on the opposite side of the paper, just as a trip up an octave of musical notes lands a musician at the same note, but one octave higher: in the same place, but not.
For a map that would represent music accurately, Tymoczko needed a shape folded once to acknowledge the circular nature of octaves, and again to reflect the existence of two different combinations that produce the same result—for example, A plus C sounds the same as C plus A. “On a piano, there are many, many different ways of playing the same chord,” Tymoczko says. “I’ve collapsed all the different ways of playing a chord into a single point on the map.”
 |  |
 |  |
Chopin’s hermetic E minor prelude, long baffling to music theorists, traces out a logical pattern of chords (as represented by the moving colored circles) in a four-dimensional orbifold. Each image (from an animation with piano accompaniment that may be viewed at http://music.princeton.edu/~dmitri/chopin3.mov) depicts one chord of the prelude. Changes in the large ball’s color indicate how evenly the chord divides the octave. Orange represents perfect evenness, blue perfect uneveness. The clustered gray balls represent possible chords that might be played next. | |
Tymoczko spends time with scientists and it was a physicist who suggested the orbifold upon hearing his description of the musical map’s properties. Tymoczko notes that physicists are forever using music as a metaphor for their work; now, he says, music can reciprocate.
Life inside an orbifold is a non-Euclidean world, meaning it doesn’t adhere to the traditional properties of geometry. One might walk in a straight line and end up back where one started, except everything is backwards. (“Like walking through the looking glass,” Tymoczko says.) With help from professor of mathematics Noam Elkies, another composer, Tymoczko worked out the mathematics behind the geometry that now allows users of a computer program (available for download on his Princeton website; see below) to map their own musical compositions.
Tymoczko has used his system to plot a variety of works in the Western musical tradition, ranging from eleventh-century Gregorian chant to more recent classical and jazz pieces. The system may not work as well with compositions that don’t consist of chord progressions, but Tymoczko says it is broadly applicable otherwise. “The idea that harmonies should sound good, that chords should be consonant rather than dissonant, is a widely shared musical value, and you find it in many different cultures,” he says.
He envisions using the mapping system to help schoolchildren understand music. Other applications might include computer programs for composing and analyzing music, and maybe even the invention of new instruments whose design makes it easy to play pleasing compositions. He is less sanguine about applications for the recording industry. “It’s probably not going to tell you why one Britney Spears song sells and another one doesn’t,” he says, because most pop music songs already consist of familiar, pleasing chords rearranged in various pleasing orders. In other words, pop music producers have already figured out, intuitively, what Tymoczko’s mapping system shows.
~Elizabeth Gudrais
Dmitri Tymoczko e-mail address: dmitri@princeton.edu
Website: http://music.princeton.edu/~dmitri